开课学院: 理学院 制作人:刘文军
课程名称 |
数学分析Ⅰ |
授课对象所属专业 |
数学与应用数学 |
课程类型 |
理论课 |
开课年级 |
2021、2022级 |
课程性质 |
专业基础必修课 |
课程总学时 |
84学时 |
一、课程简介(300字左右)
《数学分析》是数学与应用数学专业学生必修的最重要的专业基础课,也是数学专业学生考研必考的课程。它是一门比较难的课程,有其固有的特点,就是高度的抽象性、严密的逻辑性和广泛的应用性。
授课对象是数学与应用数学专业的大一本科新生,刚刚经历了高考,大部分同学都有较好的数学基础,还也有一部分同学数学功底较差,高考数学没及格。
由于本课程知识的高度抽象性和学生个体数学基础的差异性,导致学生认知和理解能力参差不齐,部分学生的学习兴趣比较低,有畏难情绪。这就需要任课老师因材施教,循循善诱,改进完善教学内容和教学方法,激发学生的主观能动性。
二、案例基本信息
1.案例名称:导数概念的严谨性
2.对应章节:第五章第1节 导数的概念
3.课程讲次:第1讲
三、案例教学目标
知识目标:了解第二次数学危机,理解导数概念的两个引入问题的解决方法和结果,通过对导数定义式的内涵与形式分析, 深入理解和掌握导数的定义。理解导数的几何意义,掌握可导与连续的关系,会用导数定义求函数导数,并会判断函数的可导性。
能力目标:培养学生的归纳总结能力,应用数学知识解决实际问题的能力。
德育目标:通过介绍牛顿和莱布尼茨对导数概念没有严谨的定义导致第二次数学危机这段数学历史,培养学生严谨的科学精神。通过介绍中国复兴号高铁瞬时速度的计算问题,引出导数的概念,激发学生的爱国情怀,从而调动学生学习导数知识的兴趣。
四、案例主要内容
主要内容:
1.导数的严谨定义,导数的几何意义,可导与连续的关系。
2.会用导数定义求函数导数,并会判断函数的可导性。
教学重点: 函数在一点处的导数概念和导函数概念。
教学难点: 判断函数的可导性。
五、案例教学设计
1.以“学生为中心"的教学环境设计
教学以学生为中心,课前学生借助教材和中国大学MOOC资源进行自主学习;课中创建宽松和谐的课堂教学环境,加强师生互动、生生互动;课后学生要自主探究完成作业、测试、报告等任务,注重发挥学生的主观能动性。这样的环境设计,有利于提升学生认真严谨、求真务实、团结合作、独立思考、勇于探索的综合素养。
2.教学方法设计
(1)问题教学法。问题教学法是教师在课堂上常用的教学策略。例如, 教师可以利用慕课堂提问、学生抢答的方式,检验学生课前线上预习与前测效果。
(2)启发教学法。教师运用启发教学法激发学生的学习兴趣。
(3)小组讨论教学法。通过小组讨论教学法培养学生团结协作、勇于探索的精神。
3.课前任务设计
教师的教学准备:1)利用慕课堂精心备课,对学生当前的学习情况和学习能力进行合理分析,制定详细的课堂教学流程。2)在中国大学慕课SPOC平台设计好学生自主学习任务,精心设计SPOC平台的学习视频、学习文档、随堂测试、单元作业、单元讨论、单元测试、课内实践报告等。3)利用中国大学MOOC的慕课堂设计课堂练习、课堂讨论、问卷、公告等环节。4)精心设计课程思政融入点和融入方法。
学生的学习准备:1)课前看教材,有目的、有重点地预习“导数的概念”的有关内容。2)课前观看在中国大学慕课上的“导数的概念”的教学视频,完成随堂测试(即课前测试)。
4. 课堂教学过程设计(90分钟)
教学环节 |
教学内容 |
时间安排 |
师生活动 |
教学方法 |
育人目标与思政元素 |
前测解析 |
1.给学生提出一些简单的基本概念问题, 以检验预习效果。如: 函数在一点可导的定义式的形式是怎样的? 函数可导与连续有什么关系? 2.分析学生前测的解答情况,讲解易错点 |
5分钟 |
以教师利用慕课堂提问、学生抢答的方式,检验学生课前线上预习与前测效果。 |
问题教学法 |
督促学生养成预习的好习惯。 培养学生自主学习的能力。 |
知识导入 |
1、引入 思政元素:介绍第二次数学危机:牛顿和莱布尼茨在创建微积分理论体系时,并没有准确定义导数的概念,产生无穷小悖论,导致了导数概念混淆不清,最终引发了第二次数学危机。 例如:对 求导数,根据牛顿的计算方法有 求导数,根据牛顿的计算方法有 。将 。将 代入上式可得: 代入上式可得: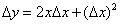 , ,   这就是无穷小悖论。 这就是无穷小悖论。
下面研究两个实际问题: 问题1: 切线的斜率 问题2: 瞬时速度
设一质点和直线运动,其运动规律为s=s(t),若t0为某一确定的时刻,t为邻近于t0的时刻,则 是质点在时间段[t0, t](或[t ,t0])上的平均速度,若t→t0时平均速度v的极限存在,则称极限 是质点在时间段[t0, t](或[t ,t0])上的平均速度,若t→t0时平均速度v的极限存在,则称极限  。 。
思政元素:以我国高铁车厢内速度显示屏为切入点,引入如何求解瞬时速度问题。介绍“高铁精神”,即:“科学求实、相容并蓄;自主创新、赶超一流;忠诚祖国、拼搏奉献。” |
15分钟 |
教师引导学生对无穷小悖论进行讨论 通过两个问题引入导数的定义式 |
启发教学 法 案例教学法 |
通过介绍数学历史,培养学生严谨的科学精神。 “高铁精神”展现在世人面前的是一道靓丽的风景线,让世界惊叹!集中体现了以爱国主义为核心的民族精神和以创新为核心的拼搏精神。借此培养学生的自信心和自豪感。 |
函数的导数概念教学 |
2、导数的定义 定义1 设函数y=f(x)在点 的某邻域内有定义,若极限 的某邻域内有定义,若极限 存在,则称函数f在点x0处可导,并称该限为函数f在点x0处的导数,记作 。 。 也可写作: 
问题:若函数 在点 在点 可导,试问 可导,试问 与 与 有何区别? 有何区别? 导数定义的关键为函数在一点处的增量与相应自变量的增量之比的极限,与增量所采用的表现形式无关,即导数的定义式可以表现为多种形式,但其本质是一样的。 思政元素:借导数的定义式可以表现为多种形式,教育学生看待事物不能只看表象,更要分析概念所反映事物的本质,内涵决定形式,而不是形式决定内涵。 |
25分钟 |
师生共同探讨研究函数在一点的连续定义式的各种等价形式。 用慕课堂点名提问 教师引导学生比较导数定义式的多种形式 |
多媒体 结合黑板 讲授 问题教学法 启发教学 法 |
培养学生抽象逻辑思维能力;提升学生分析、类比、演绎的能力,形成科学的数学素养和严谨的治学态度。 通过内涵与形式的分析,使学生更深入理解导数的定义。提高学生正确认识问题,科学分析问题的能力。 |
例 题教学 |
3、导数应用例题
例1 求函数 (x)= x2在点x=1处的导数,并求曲线在点(1,1)处的切线方程。 (x)= x2在点x=1处的导数,并求曲线在点(1,1)处的切线方程。 例2 证明函数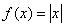 在点 在点 处不可导。 处不可导。
|
10分钟 |
教师精讲细讲,学生学习掌握解题思路 |
案例教学法 |
通过精讲例题,能让学生掌握严谨的思维方法。 |
导数理论教学 |
4、可导与连续的关系
首先,介绍 此式为 在点 在点 的有限增量公式。 的有限增量公式。 由有限增量公式式立即推得: 定理5.1 若函数 在点 在点 可导,则 可导,则 在点 在点 连续。 连续。 注1: 可导仅是函数在该点连续的充分条件,而不是必要条件,如例2中的函数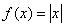 在点 处连续,但不可导。 处连续,但不可导。 注2:其逆否命题为:若函数 在点 在点 不连续,则 不连续,则 在点 在点 不可导。此命题可作为判断一个函数不可导的依据。 不可导。此命题可作为判断一个函数不可导的依据。 5、导数的几何意义 函数 的导数 的导数 是曲线 是曲线 在点 在点 处的切线斜率。 处的切线斜率。
问题:若函数在某一点不可导,则曲线在该点不存在切线。这种说法对不对? |
25分钟 |
师生共同探讨研究可导与连续的关系。 用慕课堂点名提 |
多媒体 结合黑板 讲授 问题教学法 |
培养学生抽象逻辑思维能力;提升学生分析、类比、演绎的能力,形成科学的数学素养和严谨的治学态度。 |
讨论交流 |
证明函数 仅在点 仅在点 处可导,其中 处可导,其中 为狄利克雷函数。 为狄利克雷函数。
|
9分钟 |
学生分组讨论 |
小组讨论法 |
培养学生团结协助、勇于探索的精神。 |
总结反思 |
教师对本讲“导数的概念”做总结,强调重点,突出难点、易错点。 |
1分钟 |
教师总结, 学生反思 |
反思 教学 法 |
培养学生的总结反思能力。 |
5、过程性考核评价设计:
学生回答提问和上台演板的得分最高为5分,属于线下成绩中的课堂表现成绩。由老师即时打出分数,都是记录在中国大学MOOC慕课堂学习表现的点名成绩里。
学生课堂练习的答对次数和参加讨论的次数都是记录在慕课堂学习表现的练习和讨论成绩里,因为都是用慕课堂线上完成任务,所以属于线上成绩。
6、课后任务
1.完成教材课后习题5.1的第3,4,5,6, 7,8大题。要求做在作业本上,下周一上交。2.复习5.1节,预习5.2节 。3.完成中国大学慕课SPOC第五单元的单元测验。4.参与中国大学慕课SPOC第五单元的单元讨论,讨论写在纸上,拍照上传到SPOC。
六、教学反思
本讲教学总体效果良好,通过课堂提问、演板、练习、讨论的结果反馈可知,学生能较好地理解函数导数的概念、导数的几何意义、可导与连续的关系,较好地掌握利用导数定义求函数导数、判断函数的可导性的方法。教学能较好地实现知识目标、能力目标和德育目标。
不足之处:课程思政元素内容不够丰富,不够吸引学生。课程思政体现形式单一,主要以PPT图片展示配合教师讲授的形式融入课堂。
今后本课程在课程思政方面需要在以下方面持续不断改进:
1. 不断丰富课程思政元素,把更多更好的哲学、文学、史学、科技、时政、生活、美学、音乐等知识融入到课程教学中。
2. 不断丰富课程思政融入路径,让课程思政元素在视觉、听觉上更加贴近学生。例如,老师在讲数学家的小故事时,在投影平幕上能同时出现动画,或者以短视频的形式来表达。这需要老师具备一定的动画制作能力和短视频制作能力。