知识点梳理 知识点梳理 讲清重点与难点 慕课堂辅助教学 知识点梳理 讲清重点与难点 慕课堂辅助教学 |
一．函数在一点的连续性 定义 1 设函数 在某 内有定义, 若  ，则称在点 连 续. 等价定义1 函数 在点连续的充分必要条件是 . 思考探究：由函数极限的 定义，探究函数在一点连续的精确定义 等价定义2 函数在点连续的充分必要条件: 对任给的 存在 使得当 时有 . 提问：大家可以比较函数在一点连续定义和在一点有极限的定义，说出两者的异同点。 等价定义3 在点连续  . 等价定义4 函数在 点连续的充分必要条件是: 对任何以 为极限的数列 , 都有  . 例1 证明函数 在点 连续, 其中 为狄利克雷函数. 定义2 设函数在某 内有定义, 若  则称在点右（左）连续. 定理4.1 函数在点连续的充要条件是：在点既是右连续,又是左连续.例2 讨论函数  在点的连续性.
二．间断点及其分类 函数在一点连续的三要素： (i) 在点有定义; (ii)  存在; (iii)  . 1. 间断点的定义 定义3 设函数在某 内有定义. 若在点无定义, 或在点有定义而不连续, 则称点为函数的间断点或不连续点. 提问：按此定义及上一段中关于极限与连续性之间联系的讨论, 若为函数的间断点, 则会出现哪些情形？ 2. 间断点的分类： 1）可去间断点 若  ,而在点无定义, 或有定义但 则称为的可去间断点. 例如,为 ,  的可去间断点. 提问：为什么称为“可去”间断点? 2）跳跃间断点 若函数在点的左、右极限都存在, 但  则称点为函数的跳跃间断点. 例如,整数点都是函数 的跳跃间断点, 是 的跳跃间断点. 可去间断点和跳跃间断点统称为第一类间断点, 第一类间断点的特点是函数在该点处的左、右极限都存在. 3）函数的所有其他形式的间断点, 即使得函数至少一侧极限不存在的那些点, 称为第二类间断点. 例如, 是 的第二类间断点, 是 的第二类间断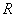点,  上每一点 都是狄利克雷函数的第二类间断点。 提问：请仔细分析一下，第二类间断点又可以细分为哪些情形？ 三．区间上的连续函数 四．若函数在区间 上的每一点都连续, 则称为上的连续函数. |
60分钟 |
师生共同探讨研究函数在一点的连续定义式的各种等价形式 由极限的精确定义，类比演绎出函数在一点连续的精确定义（连续的等价定义2） 用慕课堂点名提问，回答连续定义与函数极限定义的异同点。 用慕课堂点名请学生上来演板做题。 用慕课堂点名提问，谈谈间断点会出现几种情形？ 用慕课堂发布课堂讨论题：为什么称为“可去”间断点? 学生共同参与讨论 老师让学生举例说明第二类间断点可以细分为哪几种情形？ |
讲授法 类比 演绎 学习法 问题教学法 问题教学法 问题教学法 启发教学法 |
重点要让学生深刻理解函数在一点连续的定义以及其各种等价形式。 培养学生抽象逻辑思维能力；提升学生分析、类比、演绎的能力，形成科学的数学素养和严谨的治学态度。 引入习近平总书记在北大师生座谈会的讲话：“学习就必须求真学问，求真理、悟道理、明事情，不能满足于碎片化的信息、快餐化的知识。” 引导学生树立正确的学习观，学习过程是连续不断的、循序渐进的；对于碎片化、快餐化的知识，要分析与整合，建立知识网，内化为整体。 |
