开课学院： 理学院 制作人：蔡文娱
课程名称 |
高等数学B（下） |
授课对象所属专业 |
城乡规划 |
课程类型 |
专业基础课 |
开课年级 |
大学一年级 |
课程性质 |
公共课 |
课程总学时 |
64 |
一、课程简介
《高等数学B（下）》是经管等文科类本科专业学生的一门必修的重要基础理论课，它是为培养学生的基本素养、学习后续课程服务的。作为基础学科，高等数学具有高度的抽象性、严密的逻辑性和广泛的应用性。本课程是后续一系列应用类课程的基础，是将数学理论应用于现实问题的重要桥梁，也是适应信息时代发展需要多种领域研究的重要基石。通过本课程的学习，要使学生掌握课程内容的基本概念、基础理论和基本技能，逐步培养学生抽象概括问题的能力、逻辑推理能力、空间想象能力，熟悉的运算能力和自学能力，注意培养综合运用所学知识分析问题、解决问题的能力。
二、案例基本信息
1.案例名称：形式与内容的对立统——全微分
2.对应章节：第七章第三节
3.课程讲次：第三讲
三、案例教学目标
强化学生对数学知识的理解，提高数学的应用能力，对学生进行审美教育和辩证唯物主义教育，提高辩证思维能力，培养综合人文素养，激发学生的创造性和求知欲.
四、案例主要内容
1. 案例设计
(1)坚持情感驱动教学，让学生“亲其师、信其道”，进而愿“受其教”. 同时打造诗意课堂，促进学生 “知”、“志”协同发展。借鉴诗歌诠释数学概念、方法及所蕴含的哲理思想，通过诗歌将抽象的数学知识演奏出来，打动、感染、震撼学生的内心，让学生情感与思想自然升温，实现知识传授和思政教育有机融合，协同育人.[4]
(2)本节课结合线上和线下的资源，主要采用基于讲练式与启发式、主动学习式与讨论式等多种教学方法融合的案例教学模式.[5] 课前：敦促学生看教材、视频、慕课、进行基础练习，使其能够带着问题去听课；线上讨论与答疑，概念分析、难点互动、解题思路讨论.[5] 课中：首先由实例引出全微分的概念，再结合哲学思想讲解全微分的概念与计算. 并给出全微分的相关应用例子，由浅入深，讲练结合. 注重课堂的节奏和互动，让学生边学边做，加强讨论. 课后：线上再学习：难点学习，重点突破，讨论提升；多层训练：基础训练、综合性训练；课后案例延伸阅读：见参考文献.
五、案例教学设计
教学过程
1)问题引入
首先复习回顾一元函数的微分，指出微分是描述一元函数变化程度的工具，由此自然提出问题：当函数为多元函数时，如何描述函数的变化程度？给出实例：要在高为H=20cm半径R= 4cm的圆柱体表面均匀地镀上一层厚度为0.1cm的黄铜,问需要准备多少黄铜?由实例引出全微分的概念.
2)学习新知
定义1 如果
在定义域
的内点
处全增量
可表示为:
其中
，
不依赖于
，仅与
有关，则称函数
在点可微，
称为函数在点的全微分， 记作
．若函数在内各点都可微， 则称此函数在内可微．
注：(1)等价形式
其中
(2)函数
在点
可微Þ在点连续；逆否命题：函数点不连续Þ在点不可微.
全微分的概念中究竟蕴含了哪些真善美呢？
图1 形式与内容关系图
可微与偏导的关系：全微分的“真”
定理1(必要条件) 若函数在点可微， 则函数在该点的偏导数
必存在， 且
，即
．
证明 由函数在点可微知：
．
令
得到函数对
的偏增量
，
所以
．
同理可证
．因此有．
注：(1)习惯上，将自变量增量分别记为
，所以上式常记作：
．
通常我们把二元函数的全微分等于它的两个偏微分之和称为二元函数的微分符合叠加原理．
全微分的定义可推广到三元及三元以上函数，叠加原理也适用于二元以上函数的情况．以三元函数
为例，其全微分为
(2)定理1的逆定理不成立．即：偏导数存在，函数不一定可微!
例如：函数
在点
处由上节例4知：在处不连续，所以它在点不可微．在处偏导存在，
．由此可见：偏导数存在，函数不一定可微!
定理2(充分条件) 若函数
的偏导数在点
连续，则函数在该点可微分．
注：定理2 的逆定理不成立．即：若函数在点处可微分，不一定偏导函数在该点连续．
由此可知，多元函数连续、存在偏导数、可微的关系是：
偏导数连续
函数可微
例1设
，求（1）全微分
;（2）在点
处的全微分．
解 
，
，
例2 设
，求
．
解 
．
全可微的几何意义：全微分的“美”
当自变量增量为时，函数增量是竖坐标上的一段NQ，而二元函数在点
的全微分
的值是过P的切平面
上，当自变量分别
由增加到
时的增量，即MN那一段，于是与
之差是MQ，它的值随着
而趋于零，而且是较
高阶的无穷小量．
图2 全微分的几何意义
全微分的“美”：当
时“以平代曲” .
切面对曲面的告白，
切面与曲面的相恋，
在对立统一中实现，
你给我以平代曲的幸福，
我还你积微成博的明天.
为加深学生“以平代曲”这种微积分基本思想方法的理解，仿《切线对曲线的告白》诗句给出《切面对曲面的告白》诗句. 这样融入不仅强化学生对数学知识的理解，还让学生学习体会和欣赏数学美的艺术，促进学生情感体验和人格个性的和谐发展[6,7].
全微分在近似中的应用：微分的“善”
函数值近似值： 当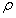很小时，
.
以平代曲的本质：扬弃了
.
微分学也是有一定的客观规律的，同学们在日常的生活和学习中也要秉承这种规律，要懂得看待事物要尊重客观规律，学会辩证的看待事物，一分为二的看待问题；也要懂得先有付出，才可能有回报，“舍”是为了 以后更广大的“得”.同时结合诗《扬弃也是一种美丽》的朗诵和歌曲《放弃也是一种美丽》的倾听，加强学生对这种辩证思维的印象.
扬弃也是一种美丽
火山放下了活跃，
是为了再次撼人心魄的喷发;
种子放下了花香，
是为了再次破土而出的希望;
扬弃就是放下，
只有懂得放下才能飞的更高;
扬弃就是舍得，
只有懂得舍弃才能抵达彼岸.[4]
例3 求
的近似值
解 设
令
由公式（3）有
例4 要在高为H=20cm半径R= 4cm的圆柱体表面均匀地镀上一层厚度为0.1cm的黄铜,问需要准备多少黄铜?
解 设黄铜的密度为 8.9g/cm3.圆柱体的体积为 
.
由于
从而所需准备的黄铜为
该例子的解决，达到首尾呼应的效果，从而让学生对全微分的知识有着深刻的印象.
3)巩固新知
(1)求三元函数 
的
(2)
4)课堂小结与思考
本节主要立足于全微分的概念以及计算，对全微分概念中蕴涵的真善美进行探索与挖掘，并借鉴诗歌诠释数学概念、方法及所蕴含的哲理思想，以诗意教学法，将思政元素渗透到整个课程教学中，使得思政教育在每一个教学环节得到体现，推动专业课程与课程思政的协同发展，为 “三全育人”教学目标的实现奠定基础，使得“教书” 与“育人”同向同行[8].
六、教学反思
本节课内容具有抽象简洁，逻辑严谨等特点，如教学方式运用不当，会让学生感觉枯燥晦涩，难以理解，打击学生的学习兴趣. 针对这个问题，本节课在教学过程中，充分挖掘数学中蕴含的中华文化和人文哲学要素，并采用诗歌教学法，以诗歌载情、以情动心，帮助学生加深理解全微分的概念与性质，并让学生学习体会和欣赏数学美的艺术，促进学生情感体验和人格个性的和谐发展.
参考文献
[1] 华东师范大学数学系. 数学分析[M]．5 版．北京：高等教育出版社，2019.
[2] 上海交通大学数学系、数学分析课程组.大学数学-数学分析[M].1 版．北京：高等教育出版社, 2007.
[3] 同济大学数学系．高等数学[M]．6 版．北京：高等教育出版社，2017．
[4] 刘珊，张丹青，侯英敏. 以微分为例高等数学课程思政案例探索与实践[J]. 教育现代化, 2021 (63):101-107.
[5] 殷志祥, 郑中团. 无穷小的概念与性质, 上海工程技术大学.
[6] 吴晖琴,周林林.大学数学课程思政的“触点”和教学体系建设 [J].现代职业教育,2020(49):112-113.
[7] 杨祥,王强,高建.课程思政是方法不是“加法”——金课、一流 课程及课程教材的认识和实践[J].中国高等教育,2020(8):4-5.
[8] 吴慧卓.高等数学教学中渗透课程思政的探索与思考[J].大学数学, 2019, 35(5): 40-43.
