《解析几何》课程思政教学案例二
(理学院:张梅)
一、课程基本信息
课程名称 |
解析几何 |
课程性质 |
专业基础课 |
学 分 |
4 |
学 时 |
56 |
开课专业 |
数学与应用数学/统计学 |
授课对象 |
大学一年级学生 |
二、课程思政典型教学案例
(一)案例名称:旋转与人生——旋转曲面
(二)教学目标
知识目标: 深入理解旋转曲面的定义、性质及旋转曲面方程的求解方法;
能力目标: 能够灵活运用旋转曲面的知识解决实际问题,增强空间想象能力和逻辑思维能力;
情感与价值目标:引导学生感悟旋转曲面中的哲学思想,培养积极向上的生活态度。通过旋转曲面的学习,激发学生探索未知、勇于挑战的精神。
(三)教学实施流程
1. 情景导入—旋转曲面的奥秘
创设情境,由生活中的实例导入旋转曲面的定义,通过生动的动画或实物模型展示旋转曲面的形成过程。
2. 新知讲授—旋转曲面的定义与方程
详细讲解旋转曲面的定义、性质,推导旋转曲面方程,通过实例和动画加深学生的理解。并引导学生思考旋转曲面在现实生活中的应用,如建筑设计、工程设计等。
3. 动手实践—旋转曲面的魅力
引导学生动手实践,利用数学软件或手工绘制旋转曲面,加深对知识点的理解,感受数学之美和旋转曲面的魅力。讨论“如何设计一个以某条给定曲线为母线的旋转曲面,使其满足特定功能需求”,鼓励学生结合专业知识,发挥创意,进行初步设计。分组展示学生的作品,进行点评和鼓励。
4. 思政育人—旋转与人生
结合旋转曲面的概念,学生作品的展示情况,引导学生思考人生哲学。将旋转曲面比作人生,母线比作人的起点或特质,准线比作人生目标或方向。引导学生思考:不同的人生起点和目标会形成怎样的旋转曲面?如何让自己的人生旋转曲面更加精彩?激励学生遇到困难,不要待在原地停滞不前,尝试着转一转,会有意想不到的收获。鼓励学生勇于面对挑战,不断突破自我,具有积极向上的生活态度。
(四)教学设计与组织实施
【学情分析】
通过对柱面、锥面的学习,学生已经对空间直线族生成曲面有了直观的认识,掌握了利用消参法求曲面方程的方法.本学时学习由空间曲线族生成曲面的方法,综合性较强,可以类比前两种曲面学习.
【教学目标】
1. 知识目标: 深入理解旋转曲面的旋转轴、母线等相关概念、性质及求旋
转曲面方程的一般步骤与方法;
2. 能力目标: 能够灵活运用旋转曲面的知识解决实际问题,增强空间想象
能力和逻辑思维能力;
3. 情感与价值目标:通过旋转曲面的学习,了解旋转曲面在生活中的应用,
享受旋转曲面之美,感受数学的魅力。引导学生感悟旋转曲面中的哲学思想,培养积极向上的生活态度,激发学生探索未知、勇于挑战的精神。
【教学重点难点】
Ø 重点:旋转曲面的相关概念、旋转曲面方程的求法。
Ø 难点:求解旋转曲面方程的分析过程。
【教学思想】
利用多媒体动态演示,以空间的一条曲线绕一条定直线旋转,可以得到一些日常生活用品的表面(水杯、雨伞等),为旋转曲面的定义埋下伏笔。同时,本设计利用由特殊到一般,由一般再到特殊的思想,引导学生理解旋转曲面的母线、轴、纬线、经线等概念。逐步观察,利用数形结合的思想探索并给出求解一般旋转曲面方程的方法。最后,利用所学知识动手实践,并探索坐标平面上的曲线绕其坐标轴旋转的旋转曲面方程,培养学生的专业素养。
【教学方法】
讲授、启发、讨论、展示等教学方法相结合。
【教学过程】
教学流程设计 |
课 题 |
旋转曲面 |
课 时 |
45分钟 |
教学手段 |
PPT与板书相结合 |
教学安排 |
教学策略 |
一、情景导入-旋转曲面的奥秘  二、新知讲授-旋转曲面的定义与方程 1.旋转曲面的有关概念 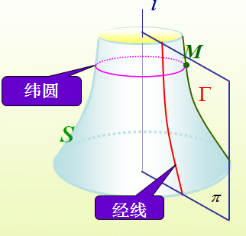
2.建立旋转曲面方程的一般方法,并举例 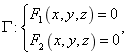
设旋转曲面的母线为 旋转轴为直线 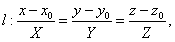 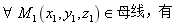 则对 则对
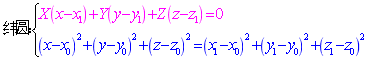
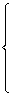
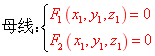
 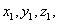 消 消 去 去
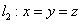 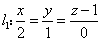
例1 求直线 绕直线 旋转所得 的旋转曲面的方程. 图形: 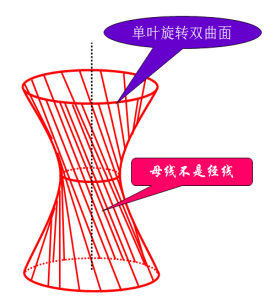
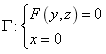 三、动手实践-旋转曲面的魅力 三、动手实践-旋转曲面的魅力
例2 设旋转曲面的母线为 ,求:⑴ 绕 轴旋 轴旋 转所得的旋转曲面方程; ⑵ 绕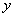 轴旋转所得的旋转面方程. 轴旋转所得的旋转面方程. 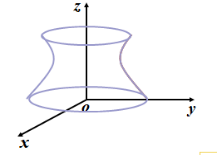
设计意图 坐标平面上的曲线绕其坐标轴旋转的旋转曲面方程是否有规律?若有,规律是什么? 规律: 一般地,当坐标面上的曲线绕此坐标面里的一个坐标轴旋转时,为求得旋转曲面的方程,只需将曲线方程保留和旋转轴同名的坐标,以其余两坐标平方和的平方根代替方程中的另一个坐标. 四、思政育人-旋转与人生 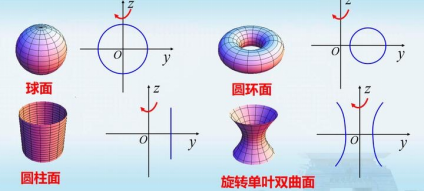
|
认知的直观性 讲清楚经线与母线的区别与联系. 抓住旋转曲面可以看成是由一个个纬圆叠加、堆积而成的思想,从而求出纬圆族方程是关键. 例1的设计,不仅学习其方程的求解方法,而且为后面单叶双曲面的直纹性的学习做铺垫. 绕谁谁不变,另一变量作代换. 将旋转曲面比作人生,母线比作人的起点或特质,准线比作人生目标或方向。引导学生思考:不同的人生起点和目标会形成怎样的旋转曲面?如何让自己的人生旋转曲面更加精彩? |
(四)教学效果及反思
通过本次课程,学生不仅掌握了旋转曲面的知识点,还深刻理解了旋转曲面中的哲学思想和探索未知的精神。思政育人点的融入使数学课程更加生动有趣,激发了学生的学习兴趣和探索欲望。
在未来的教学中,可以进一步丰富思政育人的内容和形式,如引入更多数学家的故事、开展数学文化讲座等,让数学课程更加贴近学生的生活实际和成长需求。