《数值分析》课程思政教学案例

2024年10月10日 09:08 点击：[]

开课学院：理学院制作人：吴芸

课程名称	数值分析	授课对象所属专业	数学与应用数学
课程类型	专业教育课程	开课年级	大三
课程性质	选修	课程总学时	32

一、课程简介

《数值分析》是面向数学与应用数学专业大三年级学生开设的专业核心课程，主要研究用计算机求解各种数学问题的理论、方法与软件实现的科学，它在自然科学、工程技术、经济、医学等领域都有广泛应用，是一门实用性很强的课程。

本课程基于“案例教学为主线、思政教育为基石，创新能力培养为目标”的教学理念，将课程内容整合为“5+1+1”模式，即5个教学模块，1个前沿专题汇报，1个综合项目实验，采用线上线下混合式教学模式，建立科学的形成性评价体系，以案例教学为主线，蕴含理论、应用及思政三个要素，线上线下两个维度进行螺旋上升式教学设计，使学生核心素养得到螺旋上升。

课程团队提出了“思政+ 案例”的教学改革，案例中含思政，求解中藏思政，拓展中带思政，通过分析案例、讲解知识点、求解拓展案例，实现了思政元素与专业知识的完美结合，从科学精神、专业自信、家国情怀、工匠精神等多角度激励学生，达到了教学与育人的有机统一。

二、案例基本信息

1.案例名称：

精算水温：匠心与创新的融合——常微分方程数值解法的高阶拓展及应用

2.对应章节：模块3常微分方程数值解法

3.课程讲次：第8讲次

三、案例教学目标

课程通过“水温冷却问题”案例，引导学生将实际问题转化为常微分方程数值解问题，深入理解数值解法在现实中的应用。教学中，比较欧拉法、隐式欧拉法、改进欧拉法与Runge-Kutta法的原理与优劣，培养学生的科学态度和创新精神。实际操作中，学生运用Matlab求解案例，分析误差来源，掌握数值方法的精度、稳定性和计算效率。此过程不仅锻炼了学生解决问题的能力，培养学生严谨的科学态度及勇于探索的创新精神，渗透了工匠精神。

1. 价值目标

通过导入案例“水温冷却问题”的介绍及求解，激发学生的学习兴趣，培养学生的专业自信，体会常微分方程数值解法在解决实际问题中的应用价值；通过不同数值方法的演变，要求学生对比不同算法的优劣，培养学生严谨的科学态度及勇于探索的创新精神；求解导入案例时，强调对不同步长的欧拉方法进行误差分析，渗透工匠精神，培养学生追求计算精度与效率的平衡的能力。

2．知识目标

阐述欧拉法、隐式欧拉法、改进欧拉法与Runge-Kutta法的基本原理；比较上述数值方法在求解策略上的差异；描述不同欧拉法在不同问题情境中的优势和局限，以及它们的适用条件；识别常微分方程初值问题，并选择合适的数值方法进行求解。

3．能力目标

能够读懂实际案例题意，建立数学模型，转化为相应常微分方程数值解问题；应用欧拉法、隐式欧拉法、改进欧拉法与Runge-Kutta法的Matlab程序求解高阶拓展案例，并比较分析算法优劣；估计不同数值方法的误差，分析误差的来源及其对结果的影响；评估不同数值方法在解决特定常微分方程初值问题时的精度、稳定性和计算效率。

四、案例主要内容

在室温25℃的环境中将100℃的水倒入杯中自然冷却，10分钟后水温降至70℃。如果水的温度低于55℃才可以喝，请问再过10分钟后这杯水能喝了吗？

五、案例教学设计

1. 学情分析

课程内容共5个模块，本讲是第三模块，因此学生已经具备一定的理论基础和问题求解能力。然而，学生尚不具有灵活运用matlab代码求解实际复杂问题的能力。因此，课堂中的实践环节需要由浅入深，递进式设计，帮助学生逐步掌握求解复杂实际问题的能力。

2. 思政分析

在本次课程中，我们围绕“水温冷却问题”这一实际案例展开教学，旨在通过这一具体问题的介绍与求解，激发学生的学习兴趣，培养其专业自信，并深刻体会常微分方程数值解法在解决实际问题中的广泛应用价值。同时，通过对比不同数值方法的演变，引导学生对比不同算法的优劣，培养其严谨的科学态度及勇于探索的创新精神。在求解过程中，我们特别强调了对不同步长的欧拉方法进行误差分析，以此渗透工匠精神，培养学生追求计算精度与效率平衡的能力。

思政融入点分析

● 激发兴趣与专业自信培养

导入案例的选择：“水温冷却问题”作为一个贴近生活的实际问题，能够迅速吸引学生的注意力，激发其探索未知的兴趣。通过解决这一问题，学生能够直观感受到所学知识的实际应用价值，从而增强对专业的认同感和自信心。

思政融入：在案例介绍时，可结合我国科技工作者在相关领域取得的成就，如我国在热传导研究、工业冷却技术等方面的进步，增强学生的民族自豪感和专业荣誉感。

● 科学态度与创新精神培养

数值方法的对比：通过介绍欧拉法、后退欧拉法、改进欧拉法、龙格-库塔法等不同数值方法，引导学生对比各方法的优缺点，理解算法演变背后的数学原理和工程应用需求。

思政融入：在对比过程中，强调科学研究的严谨性和创新精神。通过科学家在算法改进过程中的探索历程，如他们在面对计算精度、稳定性等问题时的坚持不懈和创新思维，激励学生勇于探索未知，敢于挑战权威。

● 工匠精神与精度效率平衡

误差分析：在求解“水温冷却问题”时，通过对不同步长欧拉方法的误差分析，引导学生理解步长选择对计算精度和效率的影响。

思政融入：通过误差分析，渗透工匠精神，强调在计算过程中追求精度与效率的平衡。可以引用工匠在制造过程中的精益求精、追求卓越的精神，鼓励学生在计算过程中不断调试、优化算法，以达到最佳的计算效果。同时，引导学生认识到，在计算科学中，精度与效率往往是一对矛盾体，需要在实际应用中根据具体需求进行权衡和取舍。

3. 教学方法

本课程采用线上线下混合式教学模式，融合多元化的教学方法，包括案例教学法、小组合作学习以及联盟对抗策略，旨在全面提升学生的理论素养和实践能力。课程评价采用形成性评价，通过学生线上的学习、讨论、分组任务、模块作业及互评，线下的随堂练习、前沿汇报、实验报告、课堂表现等教学过程的记录进行评价、反馈。

具体教学流程如下：首先，学生通过“学银在线”平台上的山东省精品在线课程进行系统的初阶理论学习。在此基础上，学生们以小组合作的形式，进行初阶实践学习，并上传实践操作视频，以展示学习成果。随后，教师在线下课堂中运用BOPPPS教学模式，引导学生深入探讨高阶理论，并开展高阶实践活动，促使学生在理论与实践的深度融合中实现能力的螺旋式提升。课后，学生们将以小组合作及联盟对抗的形式，基于本模块知识点针对导入案例和拓展案例进行深入分析与求解，通过这一过程，学生将第三次实现理论与实践能力的螺旋上升，从而全面提升自身的综合素质和解决问题的能力。

4. 课堂教学活动

课堂教学活动的具体安排如下：

① 实际案例导入

② 线上学习情况回顾

③ 课堂前测

④ 精准讲授薄弱点

⑤ 初阶案例应用讲解

⑥ 分组进行初阶案例模仿式应用并上传

⑦ 高阶理论知识拓展

⑧ 分组讨论高阶实际案例求解

⑨ 学生实时上传讨论进展，教师总结点评

阶段	教学内容	教师活动	学生活动	设计意图
课前	1、欧拉法 2、后退欧拉法 3、改进欧拉法	1、发放教学视频 2、通过学习通平台发放线上自主学习任务单、导入案例、常微分方程常见数值解法代码、教学活动时间表、分组任务	1、观看超星平台本章视频 2、小组合作，分组上传实践操作视频	要求学生线上自主学习，并完成单元测试。此时为学生第一次的理论-实践能力的训练。
课上	一、创设情境，导入实际案例（3分钟）	通过案例驱动法，导入案例，启发学生思考，使学生明确常微分方程求解的实际价值	倾听、理解、师生互动	通过导入案例激发学生的学习兴趣，培养学生的专业自信。
	二、线上学习回顾，课堂前测（5分钟）	回顾线上学习后，根据单元测试，针对性选择知识点开展课堂前测，检验学生线上自主学习情况，随后即时讲解。	有部分同学很快提交，有些同学可能左顾右盼。	通过小组前测，了解学生线上自主学习情况。
	三、精准讲解，梳理知识点（12分钟）	由教师主导，逐步讲解线上自主学习知识点、重难点、易错点。	强化同学的易错点、薄弱点。	为后续求解扫清障碍，培养学生严谨的科学态度。
	四、初阶案例应用讲解（5分钟）	通过教师回顾与讲授，让学生直观了解理论与实践是如何结合，应该如何应用。	提前已经给定代码，学生已经通过分组任务的完成具备一定能力，学生很快理解接受。	学习初阶案例求解，此时为“理论-实践”的第一次上升学习。
	五、初阶案例模仿式求解（15分钟）	深化知识点及初阶案例求解，通过APP发布随堂练习，要求小组讨论，实时拍照上传，并请代表小组讲解。	大部分学生可以参与互动，完成较好。	学生分组进行模仿式初阶案例求解，此时为“理论-实践”的第二次上升学习。
	六、高阶理论知识拓展（20分钟）	通过教师讲解和启发式问答，借助PPT演示讲解知识点，进行高阶理论知识的拓展。	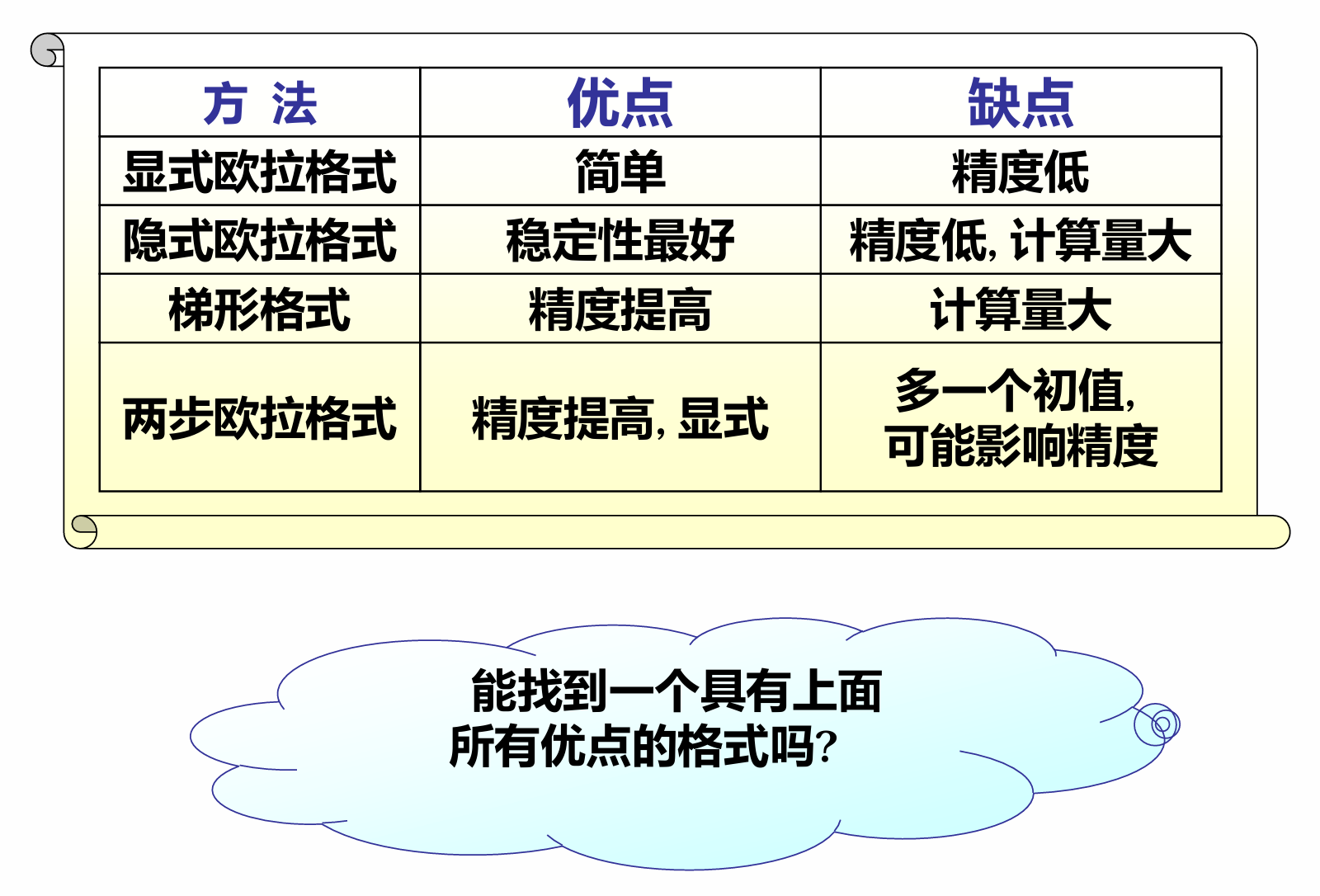倾听、理解、与教师互动。	强调科学研究的严谨性和创新精神。通过科学家在算法改进过程中的探索历程，如他们在面对计算精度、稳定性等问题时的坚持不懈和创新思维，激励学生勇于探索未知，敢于挑战权威。
	七、分组讨论高阶实际案例求解（25分钟）	小组讨论激发热情。	学生以小组为单位展开高阶实际案例的求解讨论，上机实现。	强化常微分方程数值方法高阶知识的理解与应用，培养学生科学精神
	八、学生实时上传讨论进展，教师总结点评（5分钟）	为防止有的同学“磨洋工”，要求以小组为单位，实时上传讨论进展；教师需要一直巡视，且关注各组讨论情况并进行记录；最后进行点评。	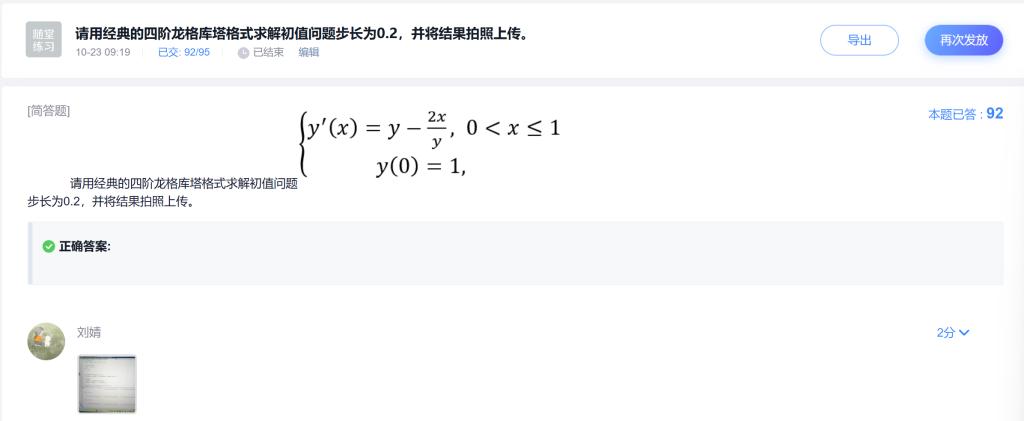有的学生会积极尝试，有的学生会偷懒	“理论——实践”的内容上螺旋上升，最后落脚于高阶开放性的拓展案例的求解，使学生能够举一反三，培养解决复杂问题的综合能力。
课后	1、高阶拓展案例的求解	1、发放实验报告要求 2、敦促学生按时提交	1、联盟对抗，以联盟为单位完成拓展高级案例的求解并提交实验报告，对抗获胜者成绩加2分。 2、完成教学模块3模块作业及互评 3、参加线上课程讨论	继续内化知识，“理论-实践”的第三次上升学习。通过误差分析，渗透工匠精神，强调在计算过程中追求精度与效率的平衡。同时，加强小组合作能力