《高等数学C》(上)课程思政教学案例
(授课单位:理学院 授课教师:吴筠)
一、课程基本信息
课程名称 |
《高等数学C》(上) |
课程性质 |
专业基础课 |
学分 |
5 |
学时 |
70 |
开课专业 |
生物科学 |
授课对象 |
大一学生 |
二、课程思政建设总体思路
《高等数学C》(上)是生物科学、药学等本科专业学生的一门必修的重要基础理论课。它是为培养学生的基本数学素养、学习后续课程服务的。本课程的主要内容包括:函数的极限与连续、导数与微分、中值定理与导数的应用、不定积分、定积分。其中一元函数的极限是学习一元函数微积分学的基础,一元函数微积分学是本课程的核心。通过本课程的学习,要使学生掌握课程内容的基本概念、基本理论和基本技能,逐步培养学生抽象概括问题的能力、逻辑推理能力和空间想象能力,注意培养运用所学知识分析问题、解决问题的能力。
《高等数学C》(上)课程思政是指在高等数学教学过程中,将思想政治教育、专业知识与高等数学学科知识相结合,培养学生的思想政治素质和科学素养。其总体思路可以从以下几个方面展开:
1.立德树人为核心目标:将立德树人作为高数数学课程思政的核心目标,通过高等数学教学,培养学生的爱国主义情怀、社会责任感、创新精神和实践能力,使学生在学习高等数学的过程中,不断提高自己的思想政治觉悟。
2.融入社会主义核心价值观:在教学过程中,融入社会主义核心价值观,引导学生树立正确的世界观、人生观和价值观,培养学生的道德品质和社会责任感。
3.强调数学的社会性和应用性:在教学过程中,强调数学知识在实际生活和社会中的应用,让学生理解数学不仅仅是一种抽象的理论,更是一种解决实际问题的工具。激发学生的学习兴趣、培养社会所需的创新型人才。
4.优化教学方法和手段:采用现代教育技术和教学方法,提高高等数学教学质量,加强师生互动,建立良好的师生关系,提高学生的学习效果。
三、课程思政典型教学案例
(一)案例基本信息
1.案例名称:”导“出综合人才,细”数“概念内涵——导数的概念
2.对应章节: 第2章 导数与微分——2.1 导数的概念
3.使用教材: 《微积分》,许成锋,马军主编,
北京航空航天大学出版社,2021.
(二)教学目标
本案例课程思政的教学目标主要有以下三个方面:
1.知识与技能目标:从概念引入的实例出发,能正确区分平均变化率和瞬时变化率;体会导数的概念体现了微积分思想的灵魂,理解导数是极限的延伸,对于发展提高数学思维有着重要的意义。
2.能力与方法目标:通过案例教学,归纳总结抽象出导数的定义式,培养
学生数学抽象、分析素养,提高学生数学运算能力,感受特殊到一般、量变引起质变的事物变化规律。体会划归思想,渗透数学意识。
3.情感态度与价值观目标:通过具体案例展示,在学生心里播下生态文明
的种子,培养学生的探索精神和创新精神,深刻体会理论与实践相结合、科学与人文相融合。结合学生专业学习需要,介绍导数在生物、医学等方面的应用,提高学生学习的自信心,帮助学生树立正确的三观,激发学生的爱国热情。
(三)教学设计与组织实施
1课前准备
1.1课前导引
引例1:九江“两湖“(甘棠湖、南门湖)综合治理工程。2023年3月6日,九江市召开了“两湖”综合治理项目发布会,正式开启了治理工程。“两湖”综合治理主要包括开展重构环湖排水系统工程、补水工程、清淤及水生态修复工程、调蓄及雨水循环中心工程、两湖岸线恢复及景观提升工程。污水处理成了这项综合治理工程的关键词。污水处理涉及到众多物理、化学和生物过程,这些过程的变化规律往往可以通过数学模型进行描述。在这些模型中,导数这个重要概念,对于理解和优化污水处理过程具有重要意义。
引例2:生态文明思想。在生态文明建设中,导数为我们提供了科学的工具和方法,帮助我们更好地理解和解决生态环境问题。譬如,通过导数分析污染物的排放趋势,可以提前预警,采取有效措施防止环境恶化;譬如,导数可以分析税收政策对资源节约和环境保护的影响,为政策调整提供数据支持。
【思政切入点】以所在城市正在进行的工程项目为切入点,以习近平生态文明思想为导向,引进微积分最重要的概念之一——导数。让学生体会到望而生畏的高等数学知识在实际生活中处处用到,在伟大的生态文明建设中处处用到,仿佛看得见摸得着,由此激发学生的学习兴趣及探索欲,培养学生关注时政,关注生态环境,增强学生的历史使命感和社会担当。


1.2课前任务
课前布置学生查阅资料,了解导数概念形成及发展史。通过学生讨论、整理出导数概念形成脉络。(1)古希腊时期:导数的概念起源于古希腊时期的数学家对于曲线的研究。例如,阿基米德在研究抛物线和圆的时候,就开始探讨曲线在某一点的切线斜率问题。(2)文艺复兴时期:随着文艺复兴的到来,艺术家们对于曲线的兴趣也推动了数学家们对导数的研究。例如,达芬奇在研究光学和力学的过程中,也涉及到了曲线切线的概念。(3)微积分的创立:到了17世纪,牛顿和莱布尼茨分别独立创立了微积分。牛顿的《自然哲学的数学原理》中,首次使用了“导数”这个词来描述曲线在某一点的切线斜率。莱布尼茨则提出了微分符号“dx”和“dy”,并给出了微分的系统理论。(4)现代发展:进入20世纪后,随着数学的发展,导数的定义和性质得到了进一步的完善。导数不仅在数学领域有广泛应用,还在物理、工程、经济、生物、医学等多个领域发挥了重要作用。




【思政切入点】首先,探索与创新。导数概念的形成和发展是数学家们不断探索和创新的结果。这体现了人类对未知世界的好奇心和求知欲,也启示我们在学习和工作中要有勇于探索、不断创新的精神。其次,科学与人文的融合。导数概念的形成不仅涉及数学领域的知识,还受到文艺复兴时期艺术家们对曲线的研究的影响。这体现了科学与人文的融合,启示我们在学习和工作中要注重跨学科的学习和思考。
2 新课导入
2.1提出问题
问题1:如何定义并求解物体做变速直线运动的速度。
问题2:如何定义并求解曲线在某点的切线。
2.2 发现规律
在解决问题1和问题2的过程中,我们抛开其物理意义和几何意义,发现都蕴含了相同的处理方式和数学结构模式。
2.3导入新课
抽象出上面的数学结构模式,引进今天的学习主题——导数的概念。我们将从导数的定义及相关定义,利用导数的定义计算导数的步骤(结合例题),导数的几何意义及反映的本质(介绍导数在生物、医学方面的应用),可导与连续的关系等几个方面把握。
【思政切入点】透过现象看本质。从不同的问题1和问题2中,我们抽象出了相同的数学结构模式。这是一种透过现象看本质的思维方式。透过现象看本质,无论是对于科研还是生活,都是一种很重要的思维方式和能力。在自然界的现象中,我们要仔细观察,收集分析相关的信息和数据,发现归纳出其中的规律和联系,进一步揭示事物的本质,逐步提高我们的科研水平。在日常生活中,我们要把错综复杂的现象,不同的观点进行比较,找出其中的共性和矛盾,深入地认识事物的本质,坚定自己正确的三观。
3 新课讲授
3.1 导数的定义及相关定义。
定义1:某点处的导数——教材第47页
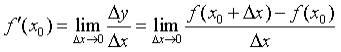
说明:
1)不同的表达方式
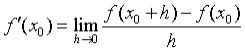
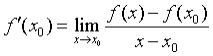
2)不同的符号记法
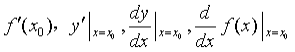
3)定义式中极限不存在,则不可导
4)概念反映的本质——函数在 处的变化率。这里可以介绍导数在生物、
处的变化率。这里可以介绍导数在生物、
医学方面的应用。譬如,药物动力学在研究药物在生物体内吸收、分布、代谢和排泄过程中,药物在体内的浓度往往随时间而变化,导数可以帮助我们理解这种变化的速度和趋势,从而优化给药方案,提高治疗效果。譬如,通过分析病人的生理数据(如心率、血压、血糖等),我们可以计算出这些数据的导数,为医生提供更准确、更全面的诊断依据。可见,导数在生物、医学方面应用非常广泛,不仅可以帮助我们更好地理解生物体内的各种复杂过程,还可以为疾病的预防、诊断和治疗提供有力的支持。


如果函数在某个区间每点都可导呢,引出导函数的定义
定义2:导函数——教材第48页
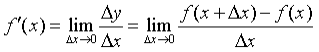
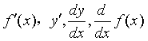
说明:
1)导函数和导数的关系, 是
是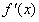 在
在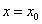 处的函数值。
处的函数值。
2)根据极限,左、右极限定义及关系定理,得出左、右导数定义及定理。
定义3:左、右导数——教材第50页
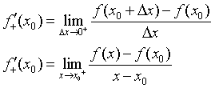
引导学生自己写出相应的左导数定义式。
定理1:可导的充分必要条件——教材第51页
 在点
在点 处可导的充分必要条件是
处可导的充分必要条件是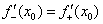
【思政切入点】通过介绍导数在生物、医学方面的应用,激发学生的求知欲,培养学生不断探索和勇于创新的科学精神。引导学生在学习和生活中,弘扬社会主义核心价值观,关注环境保护、生态平衡等问题,培养学生的社会责任感和使命感。
3.2导数的计算及几何意义
导数的计算例题——教材第47-49页
根据导数定义,归纳出利用定义计算导数的三步曲
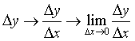
例题1 求函数 在点
在点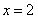 处的导数。
处的导数。
解:方法一 给自变量增量∆x时,相应地有因变量增量∆y
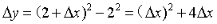
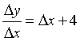
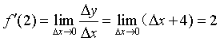
方法二 先求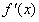 ,再代入
,再代入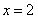 即可。
即可。
求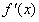 ,只需把方法一步骤中的
,只需把方法一步骤中的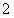 换作为
换作为 ,可得
,可得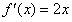
再代入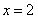 得
得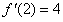 。
。
说明:
1)方法二中,如果求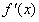 仍然用定义法,显然不如直接用方法一求
仍然用定义法,显然不如直接用方法一求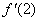 ,如果不用定义而有更简便的方法求导(函)数
,如果不用定义而有更简便的方法求导(函)数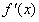 ,再求出
,再求出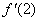 就简单得多。本章的重点就是函数的求导,这也是本章的难点。
就简单得多。本章的重点就是函数的求导,这也是本章的难点。
2)教材上其他例题在老师的提示下由学生自行完成。
3)整理所求导数,作为公式要求牢记 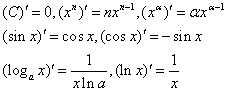
4)再回到例题1中,易知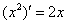 ,
,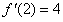 。
。
导数的几何意义——教材第50页
 就是曲线
就是曲线 在点
在点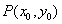 处的切线的斜率。如图
处的切线的斜率。如图
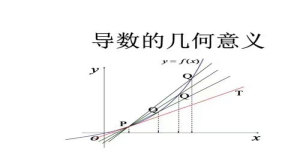
【思政切入点】结合图形来理解导数的几何意义,可以直观形象地感受到事物发展的动态过程,理解量变质变关系。鼓励学生在学习过程中,不断地积累知识和经验,逐渐提升自己的认知水平和思维能力。在认识和改造世界时,既要注重量的积累,也要关注质的变化,以实现事物的发展进步。
3.3 可导和连续的关系——教材第51页。
定理2 如果函数 在点
在点 处可导,则它在该点也连续。
处可导,则它在该点也连续。
说明:
1)证明(课堂板书推理)
2)反之,不成立。
3)例题 讨论函数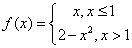 在
在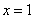 处的连续性和可导性。
处的连续性和可导性。
解:
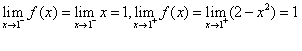
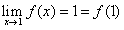 ,因此,函数
,因此,函数 在
在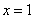 处连续。
处连续。
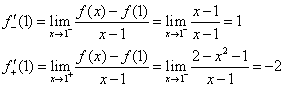
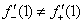 ,故
,故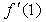 不存在,即
不存在,即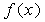 在
在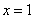 处不可导.
处不可导.
4)思考与练习 试验证函数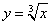 在
在 处连续但不可导.
处连续但不可导.
【思政切入点】可导与连续的关系,就像思政教育的稳定性(连续性)和时效性(可导性)。思政教育的稳定性(连续性)指的是思政教育应该保持其核心价值观和基本原则的稳定,以确保教育效果的持续性和深远影响。时效性(可导性)则强调教育内容和教育方式应该与时代背景和社会环境紧密相关,能够及时反映和应对时代的变化和挑战。这要求思政教育必须紧跟时代步伐,不断更新教育内容和方式,以适应社会的发展和变化。



(四)教学效果及反思
回顾本案例的学习过程,通过课前准备、新课导入、新课讲授等环节,让学生经历了发现、提出问题,分析、解决问题的过程;引导学生结合自身专业,多方面多角度理解导数概念的内涵及延申;通过不着痕迹地引入思政教育,让学生明白要透过现象看本质,理解量变与质变关系,弘扬社会主义核心价值观,关注环境保护、生态文明等问题,培养学生的社会责任感和使命感。
本案例教学过程中,采用了讨论法、讲授法、归纳法等。通过课前导引实例,激发学习兴趣,培养学以致用、关注生态文明的意识;通过查阅资料了解相关数学文化,让学生感受数学的理性精神、创新精神和数学家们的集体智慧。通过新课的导入和讲授,让学生体会到数学的严谨性和精准性,培养学生的数学计算、逻辑推理、数据分析等数学核心素养。
四、课程思政建设特色与创新
结合所展示的典型思政教学案例,笔者认为,《高等数学C》(上)课程思政建设可以从以下几个方面突破和创新:
1.课前准备既要有古又要有今。本案例中,课前准备分为两个阶段。首先,以所在城市正在进行的工程项目为切入点,以生态文明思想为导向,引进微积分最重要的概念之一——导数。这种着眼于眼前放眼于未来的视角既可以激发学生的求知欲,又可以增强学生的社会责任感。正所谓,脚下有路,心中有梦。其次,通过课前布置查阅资料的任务,既培养学生了自主学习能力,又让学生深刻感受数学家们的创新及探索精神,体会跨学科知识交融的重要性。
2.讲授过程既要严谨又要灵活。概念的引出要流畅、概念的讲授要严谨。计算的过程要精确,逐步培养学生的科学思维方式,提升学生数学核心素养。同时,也要因人施教因材施教,灵活整合教材知识板块、处理课堂情况。让学生在学习高等数学知识的同时,获得专业知识上的补给。提高学生的成就感、增强学生的文化自信。
3.思政教育既要有声又要无声。高数知识在实际生活中的应用(两湖治理)、在专业领域(生物、医学)方面的应用,这种看得见的应用要掷地有声地展示出来。培养学生学以致用的意识,培养新时代的综合型人才。同时,我们要有一双善于发现“思政”的眼睛,看得见细微处具体处的思政元素、润物细无声地把思政教育融入课堂,融入社会主义核心价值观,关注时政,关注生态文明,增强学生的社会责任感和使命感。